Proof pending

1. Considering infinitely many discontinuities
2. Considering functions which are discontinuous on an uncountable set
   1. The Cantor Set
   2. Cantor Indicator function and its integrability

This post came about as I was looking at Abbot’s “Understanding Analysis”. I wanted to see what more I could learn and what follows from my first two analysis courses. I am mainly using this book as reference.

Considering infinitely many discontinuities

One of the problems set after having learnt the definition of the Reimann integral, is to show that if a function has a finite number of discontinuities, it is integrable. This can be shown just by using the integrability criterion( a partition of such that ), and constructing a partition that controls the width of the intervals that contain a point where the function is discontinuous.

What about if has infinitely many discontinuities?

To begin with, the Thommae function below is an example of a function that has infinite discontinuities and is Reimann-integrable. In particular the set of discontinuities is countable, as it is discontinuous at every rational point, and continuous at every irrational point.

I’ll quickly show that it is discontinuous at every rational point. Consider (in its lowest terms). There is a sequence , such that every term is irrational and . Since , as . But . And so we see that which shows that the function is not continuous at any rational point in .

So functions that have infinite discontinuities can be integrable.

Considering functions which are discontinuous on an uncountable set

What about functions that have uncountably many discontinuities? Let be the Dirichlet function on , the indicator function for the rationals. The Dirichlet function is discontinuous everywhere, so it has uncountably many discontinuities. It is also not Reimann-integrable. We can show this by using the observation that, given any partition of , every interval formed by the partition contains irrational numbers and rational numbers, therefore the supremum and infimum of on each interval is and respectively. Therefore, and for all partitions . Therefore the lower and upper integrals are not equal, and so is not integrable.

Is it the case that all functions where the set of discontinuities is uncountable are not Reimann-integrable? Nope. I find that quite cool, as when one thinks “uncountable discontinuities”, that just feels like too many problem-points. How can there be an “area” associated with such a function?

When reading about this topic, I came across, for the first time, the Cantor set. I’m going to use it to construct a function that is discontinuous on an uncountable set of points and is also Reimann-integrable. After that example, we are going to see a criterion for Reimann-Integrability using the set of discontinuities of a function.

The Cantor Set

For a visualisation of the construction of

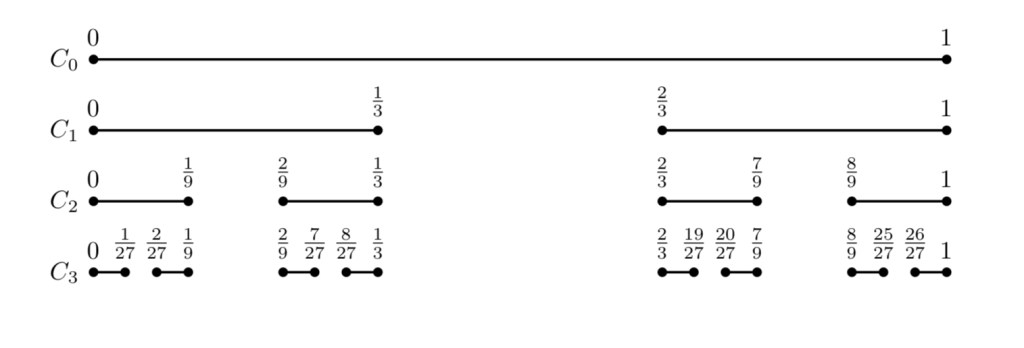
The Cantor set is uncountable, and has length zero. We can see the latter when we subtract the total of the closed intervals from the interval . .

Cantor Indicator function and its integrability

Consider the Cantor indicator function on .

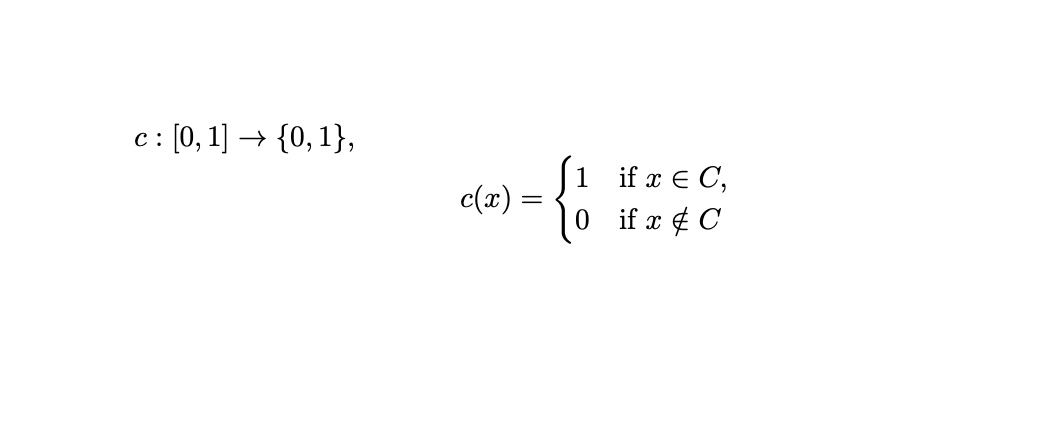
This function is discontinuous at every point and continuous at every point . (I will do a separate post covering this).

Is this function integrable on ? It is actually! Here’s a proof.