Proof pending

1. 3.1 2-connected Graphs and Subgraphs

I really enjoy graph theory as it encourages a type of problem solving that has a different flavour and is quite satisfying if you get somewhere with a question.

By no means is my knowledge very advanced but I would like to share my practice and struggles with it as it is always very formative.

I begin with a chapter of this book where the content is unfamiliar to me. I hope to branch out further and do more interesting questions as I progress.

3.1 2-connected Graphs and Subgraphs

What is a 2-connected graph? A 2-connected graph is a graph which needs at least 2 vertices to be removed in order to disconnect it.

Diestel writes that it is one of the classic results of graph theory that these two definitions for the general k-connectedness are equivalent:

• Need to remove at least k vertices to disconnect the graph
• ‘A graph is k-connected if any two of its vertices can be joined by k independent paths.

This is studied in section 3.3

We set out some terminology

• block : A block is a maximal connected subgraph without a cutvertex.

This doesn’t mean that the subgraph doesn’t contain a cutvertex of the entire graph G, but that the connected subgraph remains connected when you remove one of any of its vertices, i.e. it doesn’t have any of its own cutvertices. Hence why, as below, they can be maximal 2-connected subgraphs.

Every block is either a maximal 2-connected subgraph, a bridge with its endpoints, or an isolated vertex. Blocks are not to be confused with components. Components are disjoint, and completely determine the structure of G as they are the equivalence classes formed by the equivalence relations  if and only if there is a path from vertex  to vertex . However, blocks can intersect at no more than one vertex – a cutvertex of the graph. Diestel says how this is not such a good description of a graph as components are. This might become clear as the section goes on.

Let denoted the set of cutvertices of and the set of its blocks. forms a bipartite graph formed by the edges such that .

Here is a graph(left), and then its block graph(right).

and are all the cutvertices in the graph, as they are the only vertices which when removed disconnect this connected graph. So in other words, they are elements of the set .

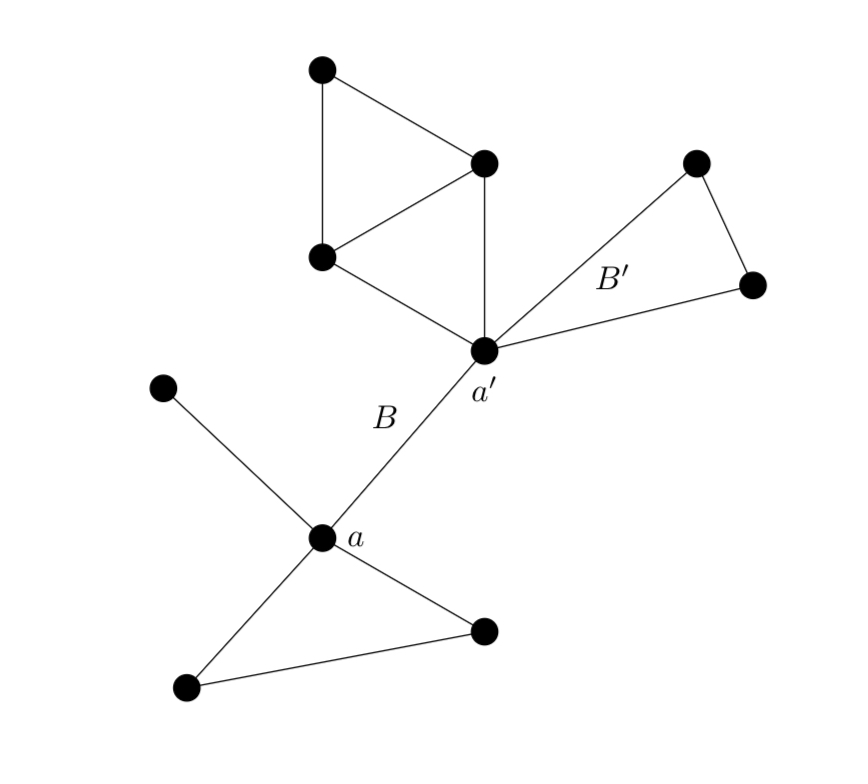
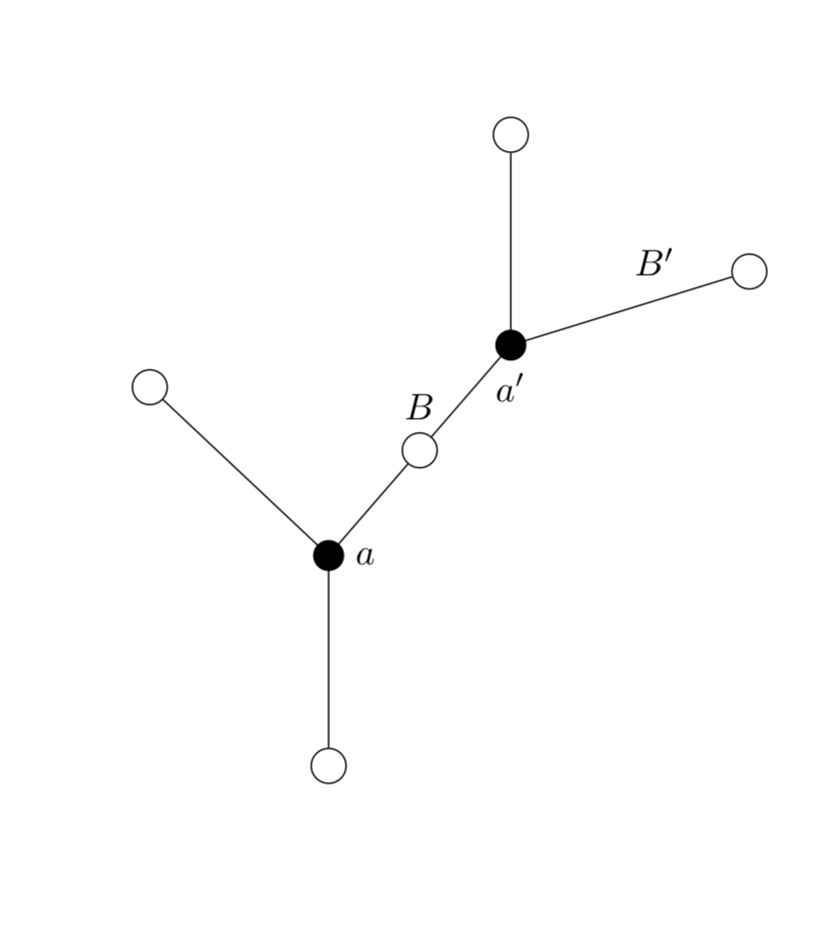
I have labelled that upper right cycle as and the bridge with its endpoints as as they are examples of blocks i.e. maximal 2-connected subgraphs. Blocks are indicated on the block graph as unfilled vertices.

The block graph of a connected graph is in fact a tree. Let’s prove.

I give a visual representation of the contradiction.

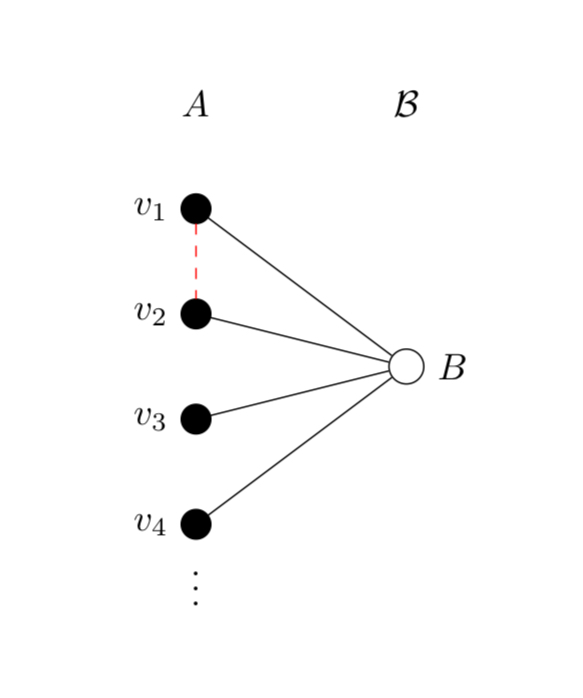
Clearly, we do not have a cycle, as cycles are paths with no repeated vertices except for the endpoints. The red dashed edge gives an example of what we could hope for if we did want a cycle, however since the graph is bipartite by its definition, we cannot have edges between any two vertices in .